Números Complexos
Clique aqui para ver o vídeo desse conteúdo!
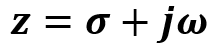
Representação na Forma Polar
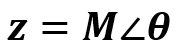
Representação na Forma Polar Exponencial
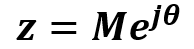
Clique aqui para ver o vídeo desse conteúdo!
[Fechar]
Representação na Forma Retangular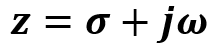
Representação na Forma Polar
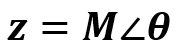
Representação na Forma Polar Exponencial
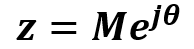
Conversões
Forma Polar para Retangular
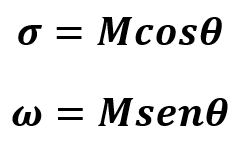
Forma Retangular para Polar
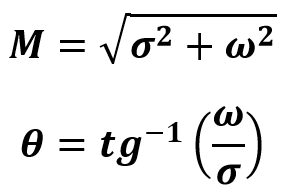
Fórmula de Euler
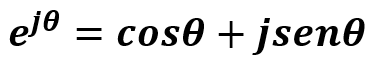
Forma Polar para Retangular
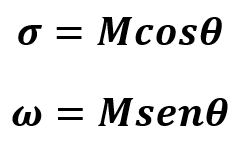
Forma Retangular para Polar
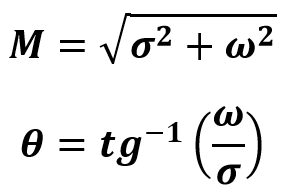
Fórmula de Euler
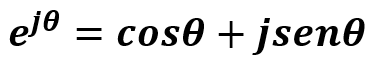
Operações com Números Complexos
Clique aqui para ver o vídeo desse conteúdo!
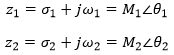
Conjugado Complexo
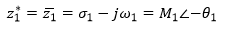
Clique aqui para ver o vídeo desse conteúdo!
[Fechar]
Considere os dois números complexos z1 e z2: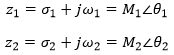
Conjugado Complexo
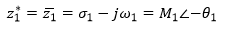
Adição e Subtração
Sempre na Forma Retangular
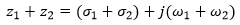
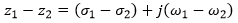
Multiplicação e Divisão
Preferencialmente na Forma Polar
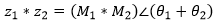
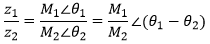
Sempre na Forma Retangular
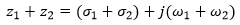
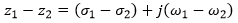
Multiplicação e Divisão
Preferencialmente na Forma Polar
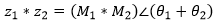
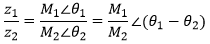
Sistemas de Controle em Malha Fechada
Clique aqui para ver o vídeo desse conteúdo!
Variável Controlada: Saída, aquilo que queremos controlar
Variável Manipulada: Entrada, aquilo que podemos ajustar

Clique aqui para ver o vídeo desse conteúdo!
[Fechar]
Sistemas de ControleVariável Controlada: Saída, aquilo que queremos controlar
Variável Manipulada: Entrada, aquilo que podemos ajustar

Sistemas com Realimentação
Sistemas Sensíveis à Saída
Set-Point (SP): Valor desejado para a Saída
Variável de Processo (PV): Saída do Sistema
Erro: Diferença do Set-Point e a Saída (SP-PV)
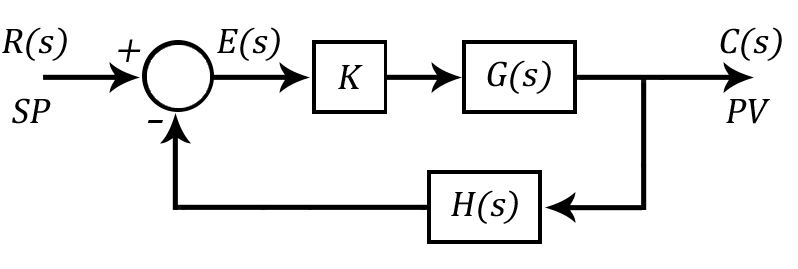
Sistemas Sensíveis à Saída
Set-Point (SP): Valor desejado para a Saída
Variável de Processo (PV): Saída do Sistema
Erro: Diferença do Set-Point e a Saída (SP-PV)

Função de Transferência em Malha Fechada
Realimentação Negativa
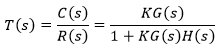
Realimentação Positiva
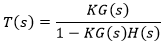
Realimentação Negativa e Unitária
Quando H(s)=1
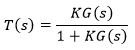
Realimentação Negativa
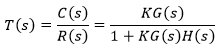
Realimentação Positiva
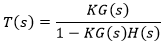
Realimentação Negativa e Unitária
Quando H(s)=1
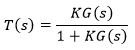
Realimentação Negativa e Unitária
Como G(s) é uma fração de polinômios, escrevemos:
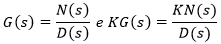
E então, fazendo as devidas substituições, temos:
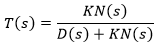
Na Prática: Basta somar o numerador no denominador da Função de Transferência em Malha Aberta que se obtem a sua correspondente em Malha Fechada (Somente quando for uma realimentação unitária e positiva).
Como G(s) é uma fração de polinômios, escrevemos:
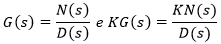
E então, fazendo as devidas substituições, temos:
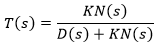
Na Prática: Basta somar o numerador no denominador da Função de Transferência em Malha Aberta que se obtem a sua correspondente em Malha Fechada (Somente quando for uma realimentação unitária e positiva).